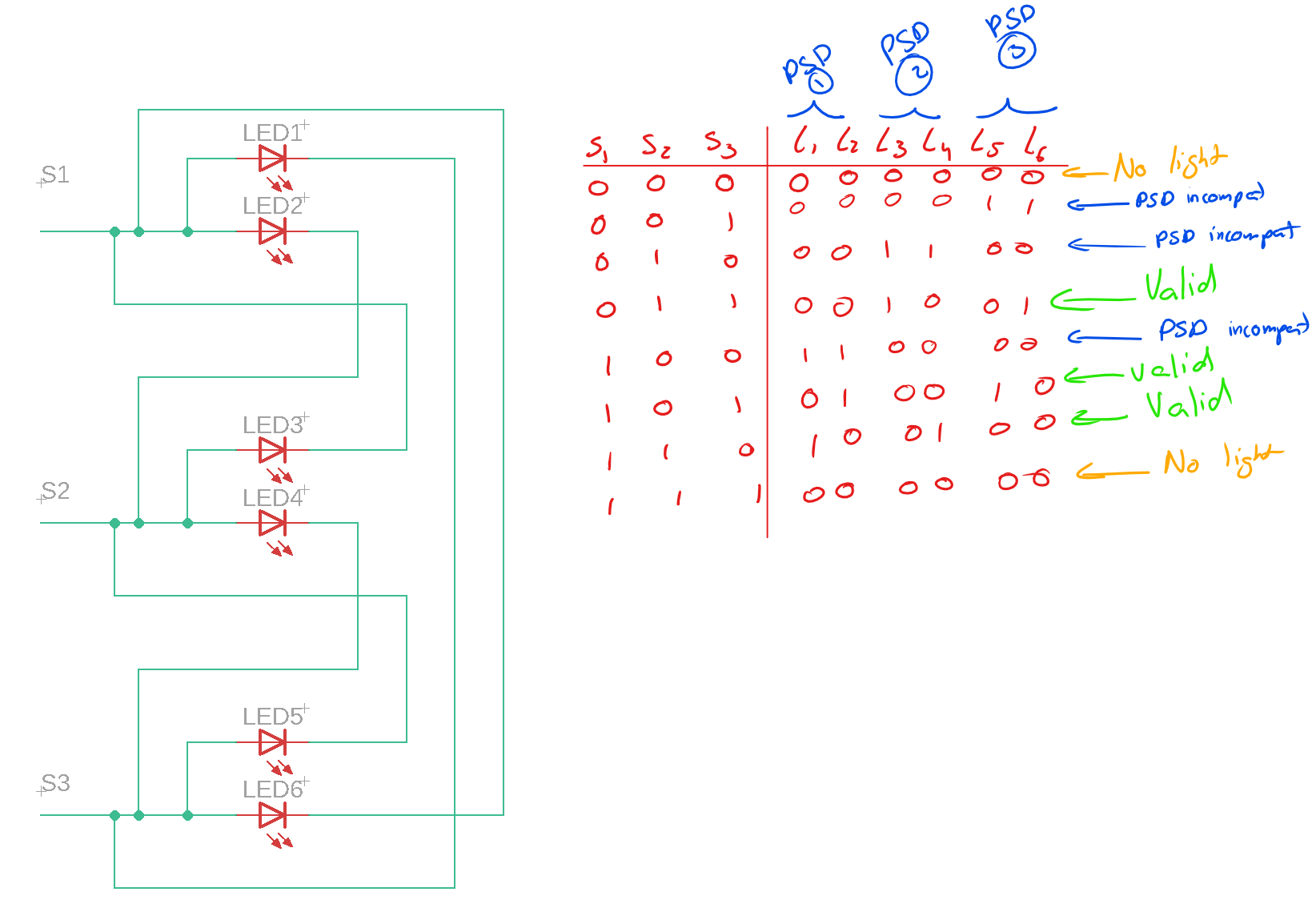
One dimensional Operation

A (1-D) PSD will output (in the form of current) the position of a light beam in a light strip. Given two linked light sources, a two degrees of freedom system can be derived. The goal is to locate the relative position of the center of both light sources with respect to the center of the PSD. i.e X_Target and Y_Target

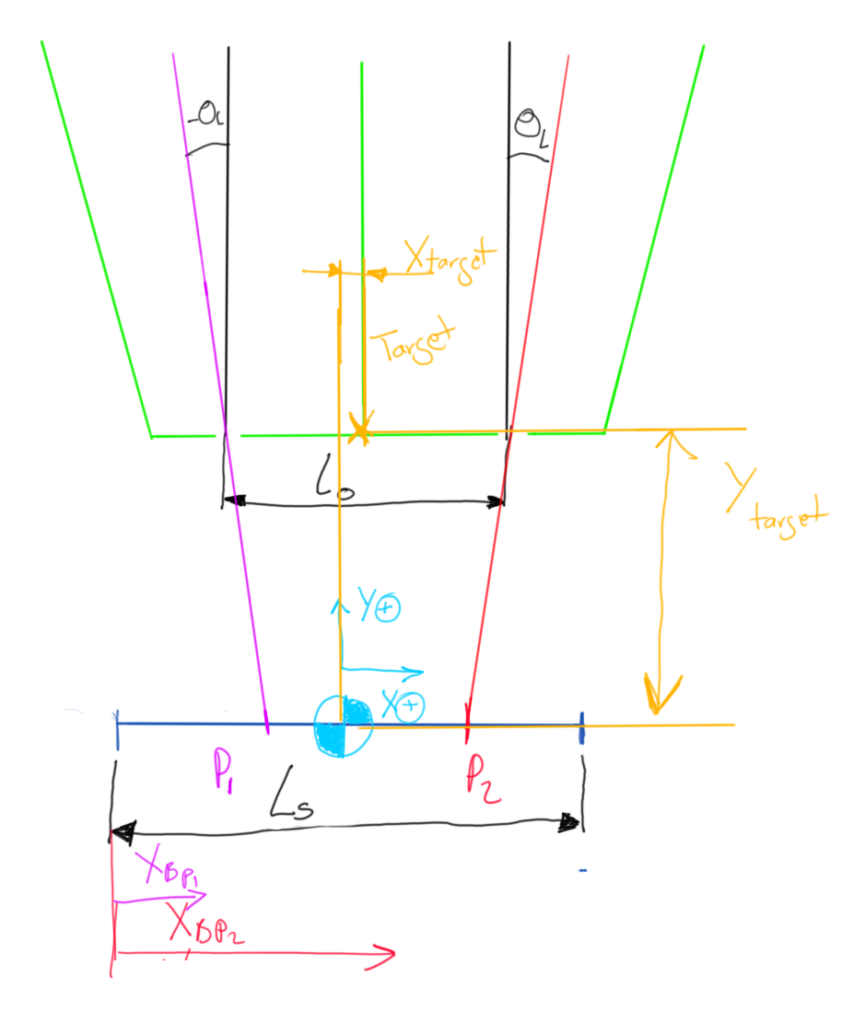
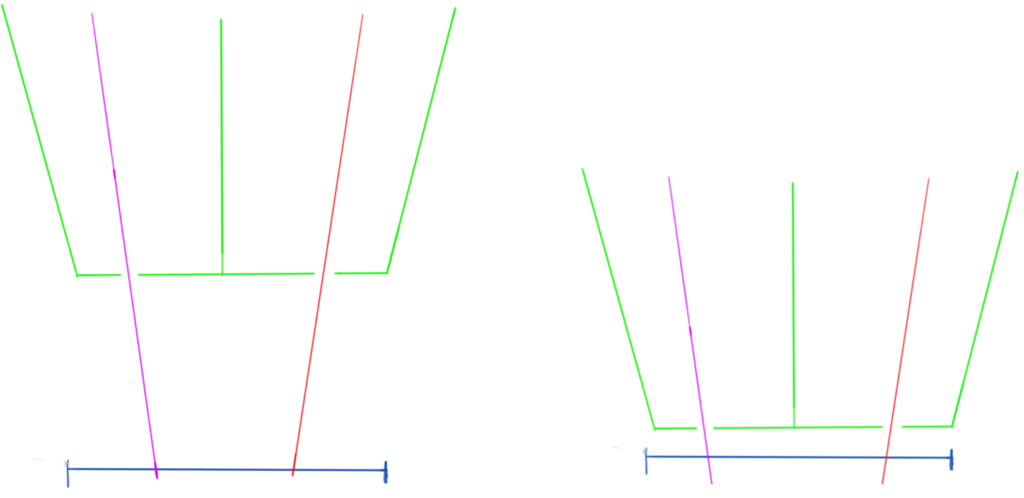
Distance to sensor

When both lights (Magenta & Red Beams) are closer, the distance between sensor and source is further away, while if both lights are closer, both lights are further apart, it, the light sources are closer to the sensor

The equation to find the distance to the sensor would be:

Y_t=L0-(XbP2-XbP1)/(2*tan(theta_L))

Position relative to sensor

The relative position is the average between both positions. This distance will be referenced from the center

X_t=(XbP1+XbP2-Ls)/2

Tree dimensional Operation

First of all, lets first define the frame of reference we will be using to determine the position

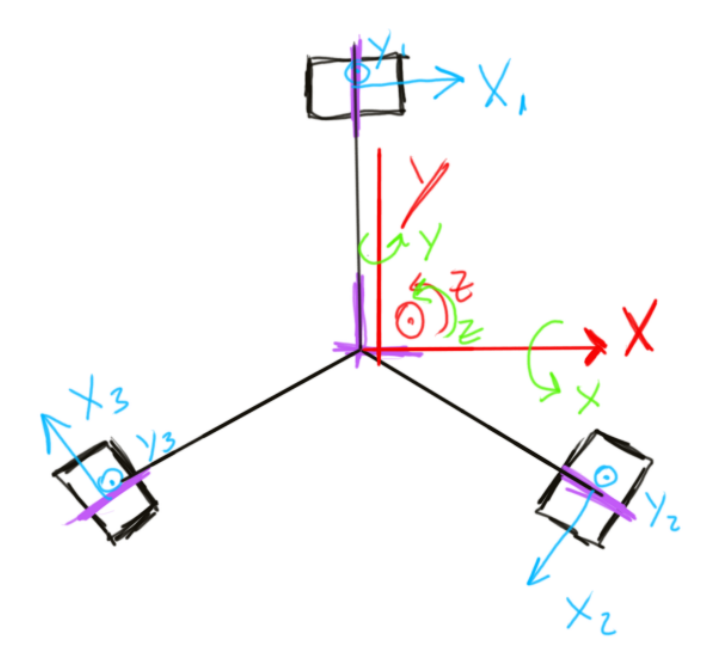
The goal is to determine the three translations and three rotations that define the position of the joystick

Translations

X direction

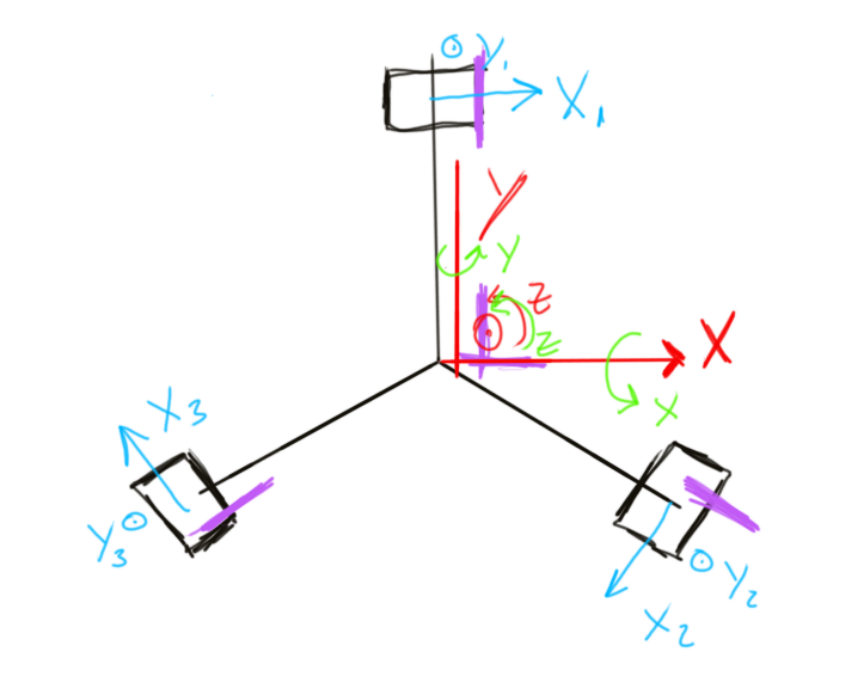
In the X direction we will average the translation of the three sensors

X=(X1*cos(90)+X2*cos(210)+X3*cos(-30))/3

Y direction

In the Y direction, sensor #1 will not see any change, therefore the equation will be as follows

Y=(X3*Sin(-30)-X2*Sin(210))/2

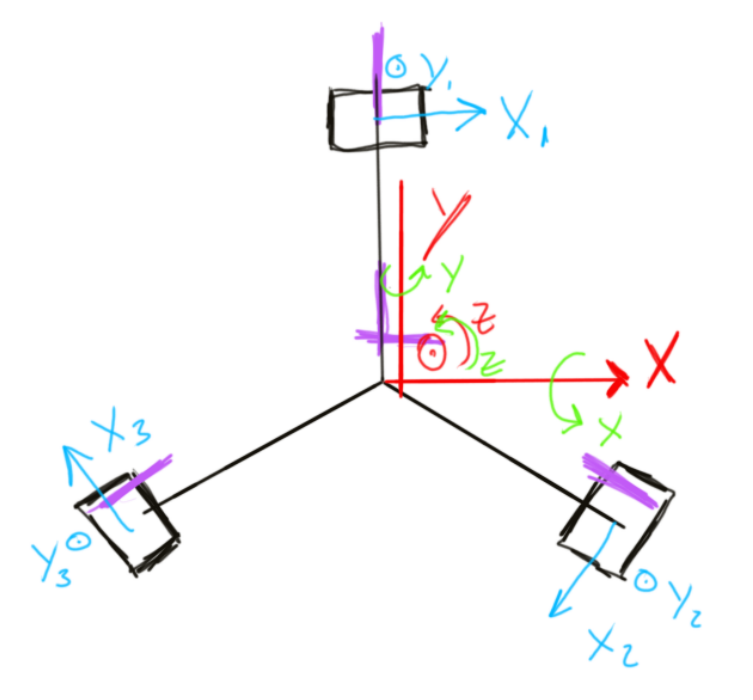
Z Direction

For The Z direction, the distance will be the average between the vertical directions of each sensor

Z=(Y1+Y2+Y3)/3

Rotations

Rotation around X

Around the X-axis, Sensor 2 and sensor 3 will see the same distance;

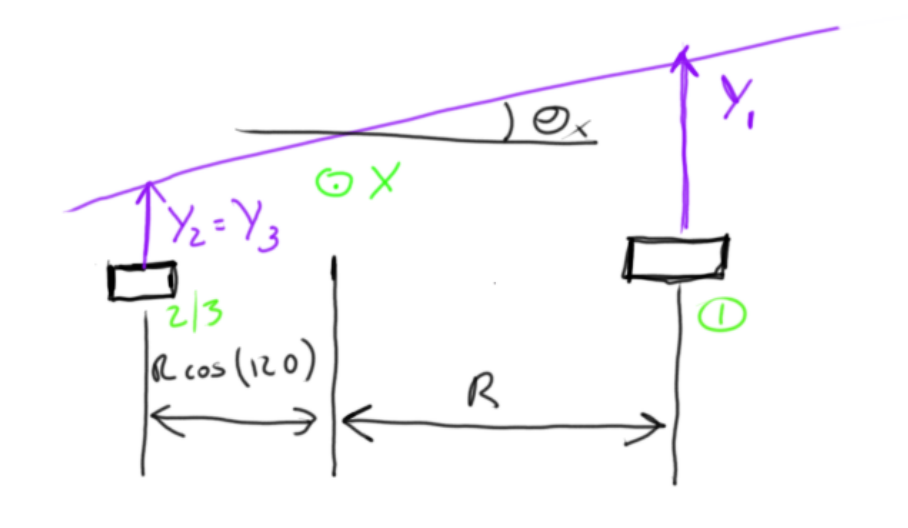
The equation will be:

Theta_X=tan^-1((Y1-((Y2+Y3)/2)))/(R+R*cos(120)))

Rotation around Y

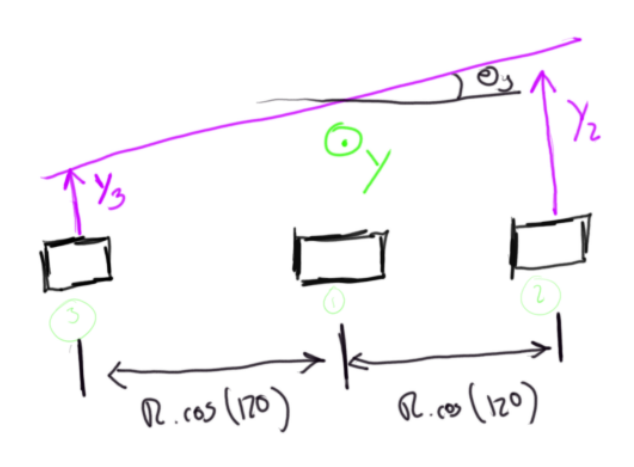
The rotation around the Y axis will be:

Theta_Y=tan^-1((Y2-Y3)/(2*R*cos(120)))

Rotation around Z

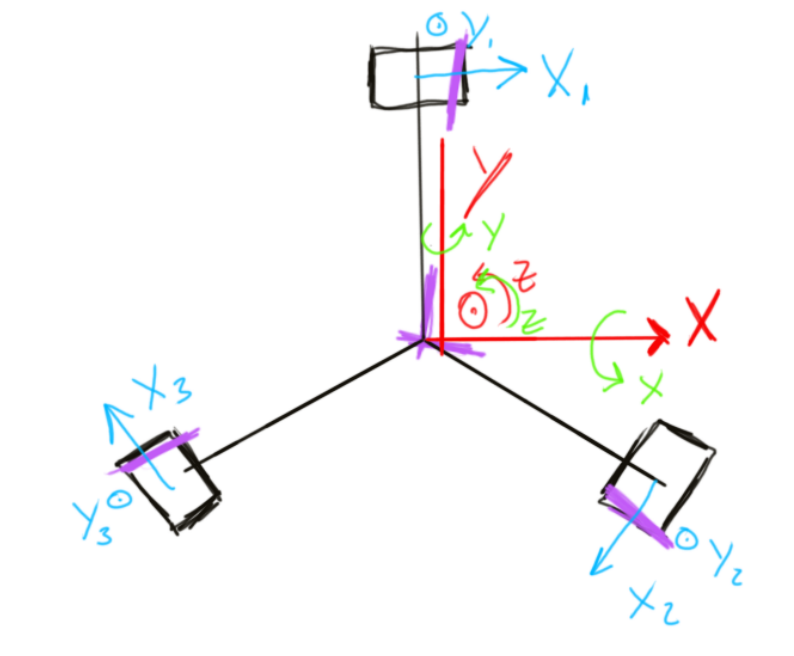
The rotation around the Z axis will be:

Theta_Z=tan^-1 (((-X1-X2-X3)/3)/R)